失蹤的正方形

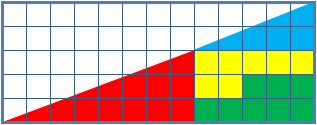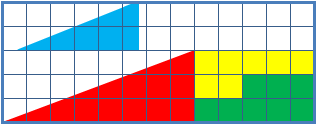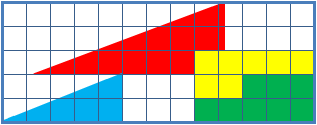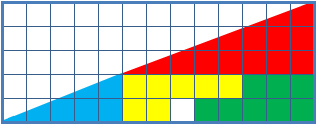
失蹤的正方形謎題是一種用於數學課的視錯覺，有助於學生對幾何圖形的思考。它描述兩種面積板塊形狀組合，每個顯然的都構成一個13X5直角三角形，不過其中一個裡頭有個1x1的孔。

這謎題的關鍵是實際上兩個13x5的多邊形並不是三角形，目測不容易察覺到紅色和藍色三角形斜邊的斜率有差別。 因此誤以為兩個組合成的圖形都是三角形。

四個圖形（黃色、紅色、藍色和綠色圖形）總共佔32個單位面積，但是外面總三角形是寬13高5，合計32.5單位。藍色三角形長寬比為5:2，紅色三角則是8:3，並且這些不是同一個長寬比。因此在每個圖中外觀上加成後的斜邊實際上縮短了。

總共縮短的長度大約是一單位的28分之一，這在此謎題示例圖上很難以看出。注意在藍色紅色斜邊交界處的網格點，如果將它與另一張圖的對應交界點比 較，邊緣稍稍溢出或者低於格點。來自兩張圖重疊後溢出的斜邊導致一個非常細微的平行四邊形，佔據了剛好一格大小的面積，恰洽是第二張圖「消失」的區域。

根據美國業餘數學大師馬丁·加德納指出，本謎題是在1953年是由紐約市業餘魔術師保羅·嘉理（Paul Curry）發明的。不過裁切悖論的原理自從1860年代就已為數學家所知了。

謎題裡描述組成圖形的整數域（2， 3， 5， 8， 13）是連續的斐波那契數。 許多其他幾何裁切謎題皆根據著名斐波那契數列的許多簡單的特質。

本謎題另類且較簡單的版本（在動畫裡顯示）使用四個相等的四邊形以及一個小正方形，則組成一個較大的正方形。當四邊形繞著其中心旋轉，中間的小正方形將被填滿，即使該圖的總面積看起來沒有變動。這外表上的悖論可由新形成的方形四邊較原來的小了一點。如果 a 代表大正方形的四邊和，且 θ 是每個四邊形相對邊間的夾角，那兩個旋轉前旋轉後方塊面積間相除的商結果是 sec²θ − 1。對於 θ = 5°，結果大約是 1.00765，故對應的差異大約 0.8%。